Consider a pressure- less distribution of non- interacting particles [ called dust ], with rest mass m and number density n in the momentarily comoving reference frame [ MCRF ] .
In a general frame the number density will go up by a factor
and
so
Thus the density 
is not a component of a four- vector.
We will see that it is a component of a 2/0 tensor.
We can introduce a number flux
four- vector 
:
where 
is the flux per unit area across a
surface with normals in the x direction etc, and 
can be interpreted as the flux across a constant ct surface.
Thus combines the flux and the number density in a
single four- dimensional quantity. Note that
The most convenient definition of the energy- momentum tensor is in terms of its components in some arbitrary frame.
where 
is the flux of 
- momentum
across a surface of constant 
. By -
momentum we mean the component of the four- momentum
.
Let us see how this definition fits in with the discussion
above. Consider first 
. This is defined as the flux
of 0- momentum [ energy divided by c ] across a surface
of constant t. This is just the
energy density .
Similarly, 
is the flux of energy divided by c
across a surface of constant 
:
Then 
is the flux of i- momentum across a surface of
constant t: the density of i- momentum multiplied
by c:
Finally 
is the j- flux of i-
momentum:
For any particular system, giving the components of 
in
some frame, defines it completely.
For dust , the components of T in the MCRF are particularly simple. There is no motion of the particles, so all i- momenta are zero and all spatial fluxes are zero. Therefore:
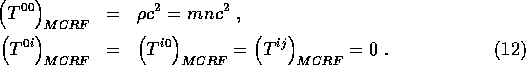
It is easy to see that the tensor 
has exactly these
components in the MCRF, where 
is the four- momentum
of a particle. It follows that, for dust we have
From this we conclude that the components of are:
or in matrix form:
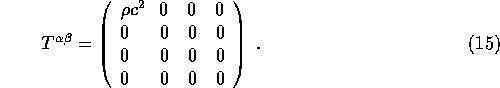
In a frame 
with 
, we therefore have
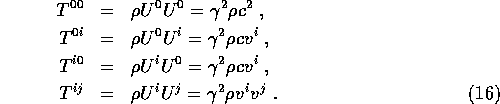
These are exactly what we would calculate from first principles, for the
energy density , energy flux ,
momentum density and momentum flux respectively.
Notice one important property of : it is
symmetric:
This will turn out to be true in general, not just for dust.